你知道吗--现代科学中的100个问题_第6节

桑舞小说网 > 科幻小说 > 你知道吗--现代科学中的100个问题作者:艾萨克·阿西莫夫

书号:41613 时间:2017/10/5 字数:1330

上一章　　　第6节　　　下一章　( → )

　　大多数人最为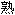

悉的数有两种，即正数（＋５，＋１７．５）和负数（－５，－１７．５）。负数是在中世纪出现的，它用来处理３－５这类问题。从古代人看来，要从三个苹果中减去五个苹果似乎是不可能的。但是，中世纪的商人却已经清楚地认识到欠款的概念。“请你给我五个苹果，可是我只有三个苹果的钱，这样我还欠你两个苹果的钱。”这就等于说：（＋３）－（＋５）＝（－２）。

　　正数及负数可以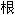

据某些严格的规则彼此相乘。正数乘正数，其乘积为正。正数乘负数，其乘积为负。最重要的是，负数乘负数，其乘积为正。

　　因此，（＋１）×（＋１）＝（＋１）；（＋１）×（－１）＝（－１）；（－１）×（－１）＝（＋１）。

　　现在假定我们自问：什么数自乘将会得出＋１？或者用数学语言来说，＋１的平方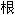

是多少？

　　这一问题有两个答案。一个答案是＋１，因为（＋１）×（＋１）＝（＋１）；另一个答案则是－１，因为（－１）×（－１）＝（＋１）。数学家是用√￣（＋１）＝±１来表示这一答案的。（碧声注：（＋１）在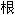

号下）

　　现在让我们进一步提出这样一个问题：－１的平方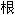

是多少？

　　对于这个问题，我们感到有点为难。答案不是＋１，因为＋１的自乘是＋１；答案也不是－１，因为－１的自乘同样是＋１。当然，（＋１）×（－１）＝（－１），但这是两个不同的数的相乘，而不是一个数的自乘。

　　这样，我们可以创造出一个数，并给它一个专门的符号，譬如说＃１，而且给它以如下的定义：＃１是自乘时会得出－１的数，即（＃１）×（＃１）＝（－１）。当这种想法刚提出来时，数学家都把这种数称为“虚数”这只是因为这种数在他们所习惯的数系中并不存在。实际上，这种数一点也不比普通的“实数”更为虚幻。这种所谓“虚数”具有一些严格限定的属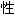

，而且和一般实数一样，也很容易处理。

　　但是，正因为数学家感到这种数多少有点虚幻，所以给这种数一个专门的符号“ｉ”(imaginary)。我们可以把正虚数写为（＋ｉ），把负虚数写为（－ｉ），而把＋１看作是一个正实数，把（－１）看作是一个负实数。因此我们可以说√￣（－１）＝±ｉ。

　　实数系统可以完全和虚数系统对应。正如有＋５，－１７．３２，＋３／１０等实数一样，我们也可以有＋５ｉ，－１７．３２ｉ，＋３ｉ／１０等虚数。

　　我们甚至还可以在作图时把虚数系统画出来。

　　假如你用一条以０点作为中点的直线来表示一个正实数系统，那么，位于０点某一侧的是正实数，位于０点另一侧的就是负实数。

　　这样，当你通过０点再作一条与该直线直角相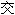

的直线时，你便可以沿第二条直线把虚数系统表示出来。第二条直线上０点的一侧的数是正虚数，０点另一侧的数是负虚数。这样一来，同时使用这两种数系，就可以在这个平面上把所有的数都表示出来。例如（＋２）＋（＋３ｉ）或（＋３）＋（－２ｉ）。这些数就是“复数”

　　数学家和物理学家发现，把一个平面上的所有各点同数字系统彼此联系起来是非常有用的。如果没有所谓虚数，他们就无法做到这一点了。ｓＡNｇｗUXｓ.ｃＯm